Космос, Excel и баскетбол на пальцах™

Многие догадываются, что размеры космоса чудовищно невообразимо и непередаваемо огромны.
Но могу поспорить, мало кто из читающих вот это самое предложение всерьез задумывались, или даже пытался посчитать лично, насколько космические расстояния действительно велики. И правильно делали, кстати. Человеческий мозг не предназначен для удержания в голове подобных величин, в него встроен специальный предохранительный механизм, который который рано или поздно обрывает полет воображения, сохраняя мозг от перегрева, а его хозяина от помещения в дурку.

Но давайте все–таки приоткроем немного двери восприятия и попробуем разобраться с космическими масштабами, а чтобы не возиться с калькулятором, воспользуемся удобным инструментом — программой Excel из пакета Microsoft Office любой версии.

От читателя не требуется практически никаких начальных знаний, что о космосе, что о работе в Excel, материал будет подан возможно даже излишне доступным языком, не фигурально, а фактически на пальцах™. От пользователя требуется лишь умение нажимать на клавиши клавиатуры и кликать левой кнопкой мышки.

Для начала представим себе, что мы взяли нашу планету Земля, средний радиус которой составляет примерно 6400 километров, на которой сейчас проживает 7 миллиардов людей, и на которой все равно еще остались места, куда не ступала нога человека, и уменьшили ее до размеров баскетбольного мяча, официальный радиус которого в профессиональных играх мужских команд равен примерно 12 сантиметров (122 миллиметра, если считать, что длина окружности 765 миллиметров).

Мысленно положите эту Землю–мяч перед собой на стол, представляя себе, какая она стала маленькая, наша планетка. А вокруг целая комната — Солнечная Система. Давайте посмотрим, каких она окажется размеров.

Запустим Microsoft Excel и глядя чистое поле таблицы, начнем вбивать буквы и цифры в ячейки.

В наших расчетах удобнее всего будет пользоваться километрами, а остальные размеры приводить к километрам.

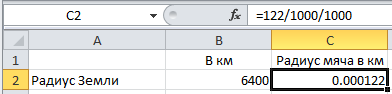
Например в ячейку радиуса Земли мы заносим 6400, а в ячейке радиуса мяча нажмем клавишу "=", затем введем "122" (радиус мяча в миллиметрах), и сразу "/1000" (разделим на тысячу, получим радиус в метрах) и еще раз "/1000", теперь нажав Enter увидим число — 0.000122 (в километрах).

Следующую колонку мы назовем "Пропорция", и в ней будем хранить отношение размера Земли к размеру баскетбольного мяча. Это удобнее всего сделать так. Кликнем мышкой в ячейку D2, нажмем клавишу "=", затем кликнем мышкой в ячейку C2 (здесь у нас хранится радиус мяча, ячейка окрасится синей рамкой), затем нажмем на клавишу разделить "/", мышкой кликнем в ячейку B2 (здесь у нас хранится радиус Земли, ячейка окрасится зеленой рамкой) и нажмем клавишу Enter.

Наверху, в стоке формул содержимое ячейки D2 окажется "=С2/B2", а в самой ячейке появится число 1.90625E–08, т.е. 1.90625х10–08, что означает баскетбольный мяч в 0.0000000190625 раз меньше, чем Земля. Позже я объясню, зачем нам нужна эта ячейка (которая впоследствии превратится в колонку) с пропорцией, а покуда просто продолжим.

Следующую колонку мы назовем "Земля–>мяч в км", т.е. здесь мы будем хранить размеры Земли, уменьшенной до размеров мяча в километрах.

Процедура уже понятная, кликнем на ячейку E2, нажмем кнопку "=", затем мышкой кликнем на ячейку D2 ("Пропорция"), кнопка разделить "/", мышкой на ячейку B2 (радиус Земли) и Enter.

Снова получаем "0.000122" в километрах. Ну, это понятно, сначала умножили на число, а потом разделили на то же число, опять получили радиус мяча, покуда ничего нового не узнали.

Для визуальной красоты и удобства восприятия добавим еще две колонки, размеры Земли, уменьшенной до размеров мяча в метрах и миллиметрах. Процедура становится прямо таки привычной. Кликаем на ячейку, кнопка "=", кликаем на предыдущую ячейку слева и клавиатурой набираем "*1000", потому что в километре 1000 метров. Получаем:

И еще раз, та же самая операция:

С чего начали, к тому вернулись. Радиус баскетбольного мяча 122 миллиметра.

Покуда все это банально, скучно и чересчур избыточно. Односложное действие мы растянули на экран текста и таблицу в семь колонок.

На калькуляторе все это можно было сделать в 10 раз быстрей, но ведь это только начало, самое интересное как раз впереди!

Начинаем исследовать окружающий космос. В самую первую колонку вбиваем интересующие нас масштабы и расстояния.

Например высоту, с которой прыгал сайдайвер Феликс Баумгартнер (гуглится по запросу "высота, с которой в прыгал сайдайвер Феликс Баумгартнер" т.е. 39 километров), высоту, на которой летают по орбите космонавты в Международной Космической Станции (подсказать, как гуглится? — 300–400 километров), расстояние Земля–Луна, Земля–Солнце и так далее.

На больших расстояниях удобно применить следующий трюк. Расстояния в Солнечной Системе удобней измерять не в километрах, в так называемых "астрономических единицах", за которую принято расстояние от Земли до Солнца. А вне Солнечной Системы удобней оперировать световыми годами или парсеками. Все эти величины легко выражаются друг через друга. Например, погуглив радиус орбиты Плутона, узнаем, что он равен примерно 40 астрономических единиц. И мы уже знаем, что делать Excel–ом в этом случае.

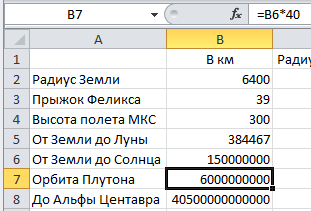
Кликаем в ячейку орбиты Плутона B7, нажимаем "=", затем кликаем в ячейку B6 (где у нас размещено расстояние от Земли до Солнца, т.е. одна астрономическая единица), а затем добавляем "*40" и Enter.

и т.д.

Теперь пошли собственно интересные трюки с Excel–ом. "Радиус мяча в км" у нас опорная величина (как и "Пропорция"). Чтобы не вбивать одну и ту же цифру 10 раз подряд, можно (и нужно) кликнуть на ячейку C2 и потянуть вниз курсором мышки за черный квадратик в правом нижнем углу рамки ячейки.

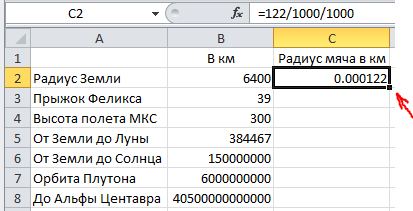
Все нижерасположенные ячейки заполнятся тем же самым числом.

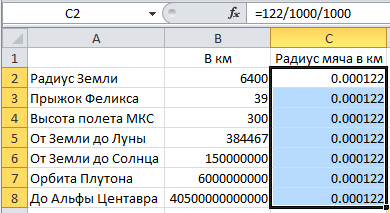
Но это еще не интересная часть. Проделаем ту же операцию для колонки "Пропорция", но тут придется немножко схитрить. Нельзя просто "растянуть вниз" ячейку D2 — получится ерунда. Нет нужды объяснять почему, дальше все само станет понятно. Проще всего на одну ячейку вниз (ячейка D3) ввести формулу "=D2", нажать Enter и растянуть вниз уже ячейку D3.

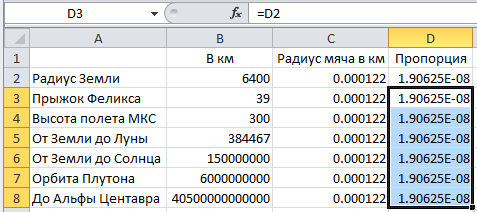
А вот теперь, наконец, интересная часть. Точно так же растягиваем вниз ячейку E2, где у нас хранились результаты сжатия размеров Земли до размеров мяча, и Ecxel сам посчитает нам все, что мы хотели и причем сразу, одним легким движением руки.

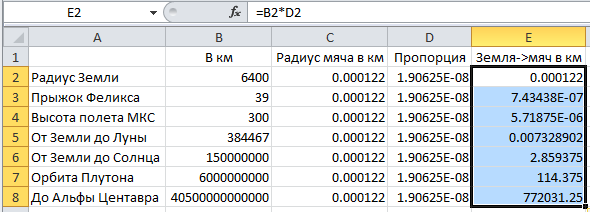
Продолжим делать тот же трюк для ячеек F2 и G2:

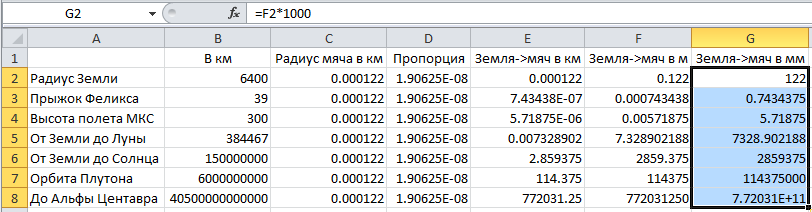
Теперь сколько бы строк (расстояний космоса) мы не поместили в первую колонку нашей таблицы (точнее мы помним — само число расстояния ставится во вторую колонку, а в первой просто имена), все они будут рассчитаны автоматически, да еще и (для удобства же) сразу и в километрах, и метрах и миллиметрах.

На этом наш урок Microsoft Excel закончен, посмотрим, что интересного принес нам космос на пальцах™.

Оказывается, что все все наши великие герои, все астронавты, космонавты и тейвонавты вместе взятые за полувековую историю покорения космоса, начавшуюся полетом Юрия Гагарина, в "модели Земля –> мяч" поднялись на 5 миллиметров над поверхностью. Чуть–чуть выше пупырышки, которая покрывает поверхность баскетбольного мяча

Про прыжок Феликса и говорить смешно, его полмиллиметра даже толщину краски на мяче не преодолели.

Выходит нету никакого "космоса" в истории человечества, мы так ничего до сих пор и не покорили. Самое великое достижение землян — шесть пилотируемых полетов к Луне и несколько вокруг Луны. Что мы имеем в нашей таблице на этот счет? Посмотрите сами, если Земля у нас размером с мяч, до Луны окажется около 7ми метров. Это огромное расстояние, по сравнению с 5ю миллиметрами орбитальных станций и неделя непрерывного полета на современных космических кораблях, которые в предлагаемом масштабе будут размерами меньше самого мелкого микроба.

А сколько в таком случае лететь до Солнца (или до Марса, что, практически, то же самое, но в другую сторону)? Почти 3 километра!

А до Плутона (который даже не граница Солнечной Системы, а так — нелепый камешек в старых учебниках астрономии)? 114 километров!

На этом расстоянии границы человеческих возможностей (и даже человеческого воображения) трагически заканчиваются.

Потому что до ближайшей звезды Альфа Центавра (на самом деле ближайшая к нам Проксима Центавра, но это мелочи) в нашем масштабе "Земля –> мяч" оказывается 772 тысяч километров, т.е. вдвое дальше, чем до реальной Луны без всяких масштабов!

Подсчет размеров нашей галактики Млечный Путь или расстояние до ближайшей к нам галактики Андромеды оставляю на ваше усмотрение и закрепление полученного материала.