Решение уравнений турбулентности...

Решение уравнений турбулентности

Подобное случалось в науке. Когда-то в глубокой древности геометры определяли отношение длины окружности к диаметру с помощью веревочки, опытным путем устанавливали зависимость площади круга от радиуса и строили великолепные колонны, умея заранее рассчитать, сколько материала для этого потребуется. Впоследствии математики научились определять число «пи» с любой степенью точности. Проводя очевидную аналогию, можно спросить: а так ли уж важно, когда будет аналитически определена постоянная Кармана? Конечно, с точки зрения теоретической это было бы блестяще. Если будет найдена замкнутая система уравнений турбулентного потока, хотя бы для пристеночного слоя (когда поток обтекает тело или стенку), то постоянная Кармана определится сама собой. А пока что это просто эмпирическая константа, и те полезные выводы, которые мы получаем и используем в механике и в геофизике, вытекают из общих соображений подобия, но без замкнутой системы уравнений.

Решение уравнений турбулентности можно найти, только наметив какие-то новые подходы к проблеме,- Их поиск, как уже говорилось, ведется в ходе разносторонних конкретных исследований.

В последние годы все шире стал развиваться метод построения математических моделей, доступных аналитическому исследованию. Система уравнений, образующая такую модель, похожа на классические уравнения гидродинамики. Такие упрощенные системы допускают аналитическое исследование. Оно проводится, чтобы выяснить основные вопросы проблемы турбулентности, например, как представить нелинейный механизм передачи энергии от потока в целом вихрям все меньшего масштаба.

Первая модель такого рода, содержащая квадратичные слагаемые (как в уравнениях Навье — Стокса), была построена голландским ученым Бюргерсом и описана им в 1938 году. На XIII Международном конгрессе по теоретической и прикладной механике был доклад о многомасштабной модели — системе дифференциальных уравнений, по своим свойствам напоминающей в основных чертах уравнения движения реальной жидкости (нелинейностью и существованием интеграла энергии). Оказывается, что в рамках нелинейных моделей уже кое-что можно сказать о механизме превращения энергии, построить такие системы типа цепочек (то есть такого вида, когда величина, определяемая первым уравнением, входит во второе, определяемая вторым — в третье и т. д.), которые показывают, как распределяется энергия между возмущениями (вихрями) различных масштабов. Такие нелинейные механизмы сейчас исследуются учеными разных стран. Для этого применяют, в частности, цифровые и аналоговые вычислительные машины; бесконечную систему уравнений, разумеется, «урезают» до конечной.

Я думаю, что такие исследования наиболее простых механизмов преобразования энергии на моделях с конечным числом степеней свободы тоже важны. Нелиний в атмосфере и океана всегда много больше, чем в технических устройствах, поэтому особенно большие числа Рейнольдса встречаются в природных турбулентных течениях.

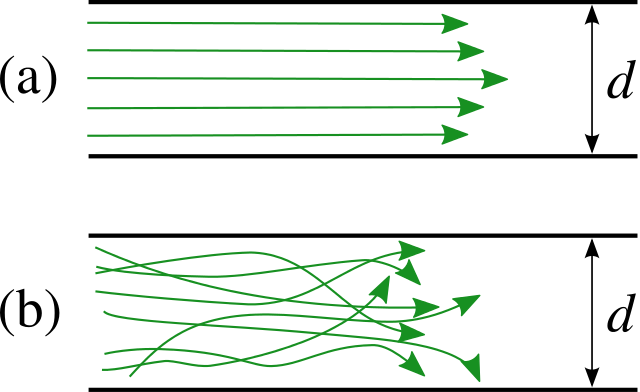
Совсем простые модели, которые позволяют продемонстрировать и понять свойства гидродинамической неустойчивости — главной причины возникновения турбулентности. В целом эта проблема очень трудна в математическом плане. Но, оказывается, можно реализовать в лабораторных условиях довольно простые случаи гидродинамической неустойчивости, что представляет несомненный интерес с точки зрения познания общих закономерностей явления.